Neural Network Feed Forward Trainable Parameters

Number of Parameters in a Feed-Forward Neural Network

Calculating the total number of trainable parameters in the feed-forward neural network by hand

Machine learning is solving such a large number of sophisticated problems today that it seems like magic. But there isn't any magic in machine learning rather it has a strong mathematical and statistical foundation.

While trying to understand the important and somewhat difficult concepts of machine learning, we sometimes do not even think about some of the trivial concepts. Maybe you think of those, but I know that I ignore a lot of simple things many a times. The reason is the amazing machine learning and deep learning libraries that have functions and methods to quickly do this for us. 😍

One such trivial problem is to find the total number of trainable parameters in a feed-forward neural network by hand. A question that I encountered in one of my exams and confused me with the options provided. This question has also been asked in many different forums by many machine learnimg practitioners. 🙋🏻

Photo by Priscilla on Unsplash

The problem discussed in this post is:

How to find the total number of trainable parameters in a feed-forward neural network?

You must be wondering why is that even an important one to discuss. It is indeed! The time taken to train a model is dependent on the number of parameters to train so this knowledge can really help us at times.

By looking at a simple network, you can easily count and tell the number of parameters. In the worst case, you can draw the diagram and tell the number of parameters. But what happens when you encounter a question of a neural network with 7 layers and a different number of neurons in each layer, say 8, 10, 12, 15, 15, 12, 6. How would you tell how many parameters are there in all?

Let us together find a mathematical formula to get the count. But before moving to the calculation, let us first understand what a feed-forward neural network is and what characteristics it possesses. This will help us in finding the total number of parameters.

A feed-forward neural network is the simplest type of artificial neural network where the connections between the perceptrons do not form a cycle.

Despite being the simplest neural network, they are of extreme importance to the machine learning practitioners as they form the basis of many important and advanced applications used today. 🤘

Characteristics of a feed-forward neural network:

1. Perceptrons are arranged in layers. The first layer takes in the input and the last layer gives the output. The middle layers are termed as hidden layers as they remain hidden from the external world.
2. Each perceptron in a layer is connected to each and every perceptron of the next layer. This is the reason for information flowing constantly from a layer to the next layer and hence the name feed-forward neural network.
3. There is no connection between the perceptrons of the same layer.
4. There is no backward connection (called a feedback connection) from the current layer to the previous layer.

Note: A perceptron is the fundamental unit of a neural network that calculates the weighted sum of the input values.

Mathematically, a feed-forward neural network defines a mapping y = f(x; θ) and learns the value of the parameters θ that helps in finding the best function approximation.

Note: There is also a bias unit in a feed-forward neural network in all the layers except the output layer. Biases are extremely helpful in successful learning by shifting the activation function to the left or to the right. Confused? 🤔 In simple words, bias is similar to an intercept (constant) in a linear equation of the line, y = mx + c, which helps to fit the prediction line to the data better instead of a line always passing through the origin (0,0) (in case of y = mx).

Let us now use this knowledge to find the number of parameters.

Scenario 1: A feed-forward neural network with just one hidden layer. Number of units in the input, hidden and output layers are respectively 3, 4 and 2.

A feed-forward neural network (Image by author)

Assumptions:

i = number of neurons in input layer

h = number of neurons in hidden layer

o = number of neurons in output layer

From the diagram, we have i = 3, h = 4 and o = 2. Note that the red colored neuron is the bias for that layer. Each bias of a layer is connected to all the neurons in the next layer except the bias of the next layer.

Mathematically:

1. Number of connections between the first and second layer: 3 × 4 = 12, which is nothing but the product of i and h.
2. Number of connections between the second and third layer: 4 × 2 = 8, which is nothing but the product of h and o.
3. There are connections between layers via bias as well. Number of connections between the bias of the first layer and the neurons of the second layer (except bias of the second layer): 1 × 4, which is nothing but h.
4. Number of connections between the bias of the second layer and the neurons of the third layer: 1 × 2, which is nothing but o.

Summing up all:

3 × 4 + 4 × 2 + 1 × 4 + 1 × 2

= 12 + 8 + 4 + 2

= 26

Thus, this feed-forward neural network has 26 connections in all and thus will have 26 trainable parameters.

Let us try to generalize using this equation and find a formula.

3 × 4 + 4 × 2 + 1 × 4 + 1 × 2

= 3 × 4 + 4 × 2 + 4 + 2

= i × h + h × o + h + o

Thus, the total number of parameters in a feed-forward neural network with one hidden layer is given by:

(i × h + h × o) + h + o

Since this network is a small network it was also possible to count the connections in the diagram to find the total number. But, what if the number of layers is more? Let us work on one more scenario and see if this formula works or we need an extension to this.

Scenario 1: A feed-forward neural network with three hidden layers. Number of units in the input, first hidden, second hidden, third hidden and output layers are respectively 3, 5, 6, 4 and 2.

Assumptions:

i = number of neurons in input layer

h1 = number of neurons in first hidden layer

h2 = number of neurons in second hidden layer

h3 = number of neurons in third hidden layer

o = number of neurons in output layer

1. Number of connections between the first and second layer: 3 × 5 = 15, which is nothing but the product of i and h1.
2. Number of connections between the second and third layer: 5 × 6 = 30, which is nothing but the product of h1 and h2.
3. Number of connections between the third and fourth layer: 6 × 4 = 24, which is nothing but the product of h2 and h3.
4. Number of connections between the fourth and fifth layer: 4 × 2= 8, which is nothing but the product of h3 and o.
5. Number of connections between the bias of the first layer and the neurons of the second layer (except bias of the second layer): 1 × 5 = 5, which is nothing but h1.
6. Number of connections between the bias of the second layer and the neurons of the third layer: 1 × 6 = 6, which is nothing but h2.
7. Number of connections between the bias of the third layer and the neurons of the fourth layer: 1 × 4 = 4, which is nothing but h3.
8. Number of connections between the bias of the fourth layer and the neurons of the fifth layer: 1 × 2 = 2, which is nothing but o.

Summing up all:

3 × 5 + 5 × 6 + 6 × 4 + 4 × 2 + 1 × 5 + 1 × 6 + 1 × 4 + 1 × 2

= 15 + 30 + 24 + 8 + 5 + 6 + 4 + 2

= 94

Thus, this feed-forward neural network has 94 connections in all and thus 94 trainable parameters.

Let us try to generalize using this equation and find a formula.

3 × 5 + 5 × 6 + 6 × 4 + 4 × 2 + 1 × 5 + 1 × 6 + 1 × 4 + 1 × 2

= 3 × 5 + 5 × 6 + 6 × 4 + 4 × 2 + 5 + 6 + 4 + 2

= i × h1 + h1 × h2 + h2 × h3+ h3 × o + h1 + h2 + h3+ o

Thus, the total number of parameters in a feed-forward neural network with three hidden layers is given by:

(i × h1 + h1 × h2 + h2 × h3 + h3 × o) + h1 + h2 + h3+ o

Thus, the formula to find the total number of trainable parameters in a feed-forward neural network with n hidden layers is given by:

Formula to find the total number of parameters in a feed-forward neural network (Image by author)

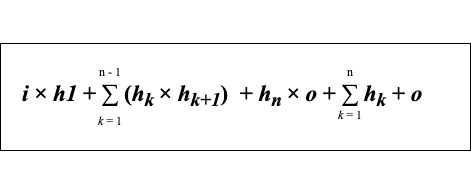
If this formula sounds a bit overwhelming 😳, don't worry, there is no need to memorize this formula 🙅. Just keep in mind that in order to find the total number of parameters we need to sum up the following:

1. product of the number of neurons in the input layer and first hidden layer
2. sum of products of the number of neurons between the two consecutive hidden layers
3. product of the number of neurons in the last hidden layer and output layer
4. sum of the number of neurons in all the hidden layers and output layer

Now, I hope you can apply this method to find the total number of parameters in a feed-forward neural network with any number of hidden layers and neurons even without using the library. 🙃

crottythorm1942.blogspot.com

Source: https://towardsdatascience.com/number-of-parameters-in-a-feed-forward-neural-network-4e4e33a53655

Share this post